Problem Statement:
Understanding the multifaceted factors influencing ball range remains a critical challenge. In this regression analysis assignment, we address the complexities surrounding rubber band positions, cup placements, and ball types through a rigorous Design of Experiments (DOE) approach. We aim to decipher the intricate interplay of these variables and provide insights that contribute to a deeper comprehension of ball range dynamics.
Introduction
Our experiment delves into the fascinating world of rubber bands, cups, and balls, exploring the factors that influence the range of throws. By conducting a Design of Experiment (DOE), we aim to unravel the mysteries behind the throw distance and identify key variables affecting it. The experimental factors, outlined in Table 1 (Bontempo, Carandente, & Manna, 2021), include rubber band position, cup position, and two types of balls—golf and squash.
| Design | Low Level | High Level |
|---|---|---|
| Rubber Band Position | 210 | 290 |
| Cup position | 285 | 325 |
| Balls | Golf | Squash |
| Response Variable | Range |
Table 1: Experimental factors and response variables
Objectives
- Identify influential factors in ball range.
- Characterize the predictor-response relationship using regression.
- Investigate potential interactions among factors.
- Establish optimal factor combinations for maximizing ball range.
Hypotheses
- Squash balls exhibit a higher range.
- Golf balls achieve the highest range.
- Rubber band and cup position impact the range.
Materials and Methods
We designed a full factorial experiment (2^3) involving rubber band position, cup position, and ball type, resulting in sixteen runs (Table 2). Randomization in Minitab was employed to minimize bias. Uncontrolled variables were addressed through randomization (Chong, et al., 2021), and systematic errors related to Range (R) were mitigated by stabilizing readings.
| RunOrder | CenterPt | Blocks | Rubber Band Pos | Cup | Ball | Range ( R ) |
|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 290 | 325 | Squash | 2370 |
| 2 | 1 | 2 | 290 | 285 | Golf | 3500 |
| 3 | 1 | 2 | 210 | 325 | Squash | 1940 |
| 4 | 1 | 2 | 210 | 325 | Golf | 1980 |
| 5 | 1 | 2 | 290 | 285 | Squash | 5000 |
| 6 | 1 | 2 | 210 | 285 | Golf | 4250 |
| 7 | 1 | 2 | 210 | 285 | Squash | 3500 |
| 8 | 1 | 2 | 290 | 325 | Golf | 2190 |
| 9 | 1 | 1 | 290 | 325 | Squash | 1945 |
| 10 | 1 | 1 | 290 | 285 | Golf | 2890 |
| 11 | 1 | 1 | 210 | 325 | Squash | 1760 |
| 12 | 1 | 1 | 210 | 325 | Golf | 1840 |
| 13 | 1 | 1 | 290 | 285 | Squash | 4500 |
| 14 | 1 | 1 | 210 | 285 | Golf | 3090 |
| 15 | 1 | 1 | 210 | 285 | Squash | 3750 |
| 16 | 1 | 1 | 290 | 325 | Golf | 2030 |
Table 2: DOE Summary
Measurement Method
The experiment measured ball range using various tools, including tape. Each run underwent meticulous cleaning, and measurements were realigned to ensure accuracy. Rubber bands, cups, golf balls, and squash balls constituted the materials.
Factor Levels
Ball range had two levels—low and high—based on literature suggesting their impact on systematic error. Golf balls represented the low level, while squash balls represented the high level due to differences in mass and velocity (El Deeb, Silva, Junior, Hanafi, & Borges, 2021).
Confirmation Runs
Confirmation runs were conducted to validate the model at its optimum, following the same method with rubber bands, cups, and balls.
Results
The regression equation, presented in uncoded units, along with the ANOVA, Pareto Chart, Main Effects Plot, Interaction Plot, and Residual Plots, summarizes our findings.
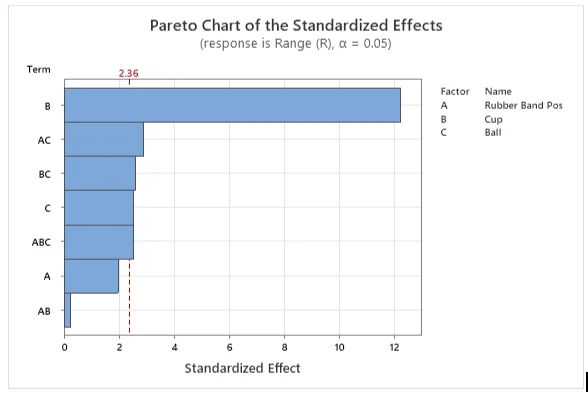
Table 3: Pareto Chart of Models
Final Model Analysis
The Pareto chart and ANOVA reveal the significance of terms in the final model (Rubber bands, Cups, Balls, and their interactions). The model selection process, supported by p-values and t-statistics, ensures the inclusion of significant variables (Alkiayat, 2021). The adjusted 𝑅-square value of 92.28% attests to the model's explanatory power. Residual plots confirm the model's validity, indicating normal distribution, equal variance, and independence of residuals.
Main Effects Plot
The main effects plot highlights the impact of the cup position, indicating higher extraction rates and increased ball range compared to the rubber band position. Unexpected results in the range factor suggest a complex interplay between rubber bands and cup position, both enhancing ball range (Alkiayat, 2021).
Interaction Plot
The interaction plot reveals varying effects when the rubber band position and cup position are held constant, emphasizing a strong interaction between the rubber band and cup. The distinct lines suggest that cup position influences range differently when rubber band position changes, indicating potential compaction effects on particle size (Rehman, Munir, Raza, & Saeed, 2021).
Cube Plot
The cube plot identifies the optimum conditions for the maximum range (4732.19) with a squash ball and a higher rubber band position. Confirmation runs at these conditions reinforce the model's adequacy and generalizability. Blocks (golf ball and squash ball) prove statistically insignificant, aligning with expectations (Alkiayat, 2021).
Conclusion
Rubber band position, cup position, and ball type emerge as statistically significant factors influencing ball range. The regression model, Range = 14055 + 10.4 rubber band position – 39.5 cup – 16026 ball – 0.0223(Rubber band position cups) + 76.5 (rubber band positionball)+ 48.8 cupball- 0.223 rubber bandscups*balls, confirms balls yield the highest range (4732.19). Hypotheses on ball range, rubber band position, and cup position are validated, except for the golf ball hypothesis.
The experiment's limitations include equipment constraints affecting measurement consistency. Future trials should employ appropriate equipment, consider quantitative measurements, increase replicates, and explore different ball properties for a more comprehensive analysis.
Bibliography
- Alkiayat, M. (2021). A Practical Guide to Creating a Pareto Chart as a Quality Improvement Tool. Global Journal on Quality and Safety in Healthcare, 83-84.
- Bontempo, R., Carandente, R., & Manna, M. (2021). A design of experiment approach as applied to the analysis of diffuser-augmented wind turbines. Energy Conversion and Management, 113924.
- Chong, B. W., Othman, R., Putra Jaya, R., Mohd Hasan, M. R., Sandu, A. V., Nabiałek, M., et al. (2021). Design of experiment on concrete mechanical properties prediction: a critical review. Materials, 1866.
- El Deeb, S., Silva, C. F., Junior, C. S., Hanafi, R. S., & Borges, K. B. (2021). Chiral capillary electrokinetic chromatography: Principle and applications, detection and identification, design of experiment, and exploration of chiral recognition using molecular modelling. Molecules, 2841.
- Purwa, T. (2021). An Alternative Procedure to Produce a P-Spline Small Area Estimation Model Based on Partial Residual Plot and Significance Test of Spline Term. Journal of Physics: Conference Series, 012040.
- Qattawi, A. (2018). Investigating the effect of fused deposition modeling processing parameters using Taguchi design of experiment method. Journal of Manufacturing Processes, 164-174.
- Rehman, F., Munir, H., Raza, M. A., & Saeed, A. (2021). Uncover the salt tolerance potential of accessions based on photosynthetic attributes and interaction plot in tomato (Solanum lycopersicum). Plant Breeding, 130-141.
Appendices
Coded Cofficients
| Term | Effect | Coef | SE | Coef | T - Value | P - Value | VIF |
|---|---|---|---|---|---|---|---|
| Constant | 2908.4 | 73.8 | 39.43 | 0 | |||
| Blocks | |||||||
| 1 | -182.8 | 73.8 | -2.48 | 0.042 | 1 | ||
| Rubber Band Pos | 289.4 | 144.7 | 73.8 | 1.96 | 0.091 | 1 | |
| Cup | -1803.1 | -901.6 | 73.8 | -12.22 | 0 | 1 | |
| Ball | 374.4 | 187.2 | 73.8 | 2.54 | 0.039 | 1 | |
| Rubber Band Pos * Cup | -35.6 | -17.8 | 73.8 | -0.24 | 0.816 | 1 | |
| Rubber Band Pos * Ball | 426.9 | 213.4 | 73.8 | 2.89 | 0.023 | 1 | |
| Cup " Ball | -380.6 | -190.3 | 73.8 | -2.58 | 0.036 | 1 | |
| Rubber Band Pos * Cup Ball | -373.1 | -186.6 | 73.8 | -2.53 | 0.039 | 1 |
Model Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
| 295.075 | 96.40% | 92.28% | 81.18% |
Analysis of Variance
| Source | DF | Adj SS | Adj MS | F -Value | P -Value |
|---|---|---|---|---|---|
| Model | 8 | 16305700 | 2038213 | 23.41 | 0.000 |
| Blocks | 1 | 534727 | 534727 | 6.14 | 0.042 |
| Linear | 3 | 13900617 | 4633539 | 53.22 | 0.000 |
| Rubber Band Pos | 1 | 334952 | 334952 | 3.85 | 0.091 |
| Cup | 1 | 13005039 | 13005039 | 149.36 | 0.000 |
| Ball | 1 | 560627 | 560627 | 6.44 | 0.039 |
| 2-Way Interactions | 3 | 1313467 | 437822 | 5.03 | 0.036 |
| Rubber Band Pos *Cup | 1 | 5077 | 5077 | 0.06 | 0.816 |
| Rubber Band Pos *Ball | 1 | 728889 | 728889 | 8.37 | 0.023 |
| Cup Ball | 1 | 579502 | 579502 | 6.66 | 0.036 |
| 3-Way Interactions | 1 | 556889 | 556889 | 6.40 | 0.039 |
| Rubber Band Pos Cup *Ball | 1 | 556889 | 556889 | 6.40 | 0.039 |
| Error | 7 | 609486 | 87069 | ||
| Total | 15 | 16915186 |