+1 (315) 557-6473 

Comprehensive Analysis of Principal Component Analysis in Statistics: Matrix Operations, Eigenvectors, and Covariance

Explore a detailed examination of Principal Component Analysis assignment (PCA) in statistics through matrix operations, eigenvectors, and covariance calculations. This comprehensive analysis covers matrix multiplication conformability, the conformability of b=(Yw)', the interpretation of the first principal component, variance and covariance computations, and the orthogonality of eigenvectors. Delve into the intricate relationships within PCA and gain a profound understanding of its key components.

  1. Home
  2. The Link Between Statistical Insights and Matrix Operations in PCA

Problem Description:

Given a dataset represented by a matrix Y of dimensions n×2, where n is the number of data points from a bivariate distribution. We have a covariance matrix S of dimensions 2×2, eigenvectors U of dimensions 2×1, and a few properties of matrix multiplication.

Solution:

Q1. Matrix Multiplication Conformability:

Problem Description: The assignment involves matrices Y (n×2), S (2×2), W (2×1), and U (2×1). Explore the conformability of matrix multiplication and determine which products are valid based on given properties.

  • YW is conformable, n = p = 2
  • YW’ is not conformable, n = 2, p = 1
  • UU’ is conformable, n = 1, p = 1
  • U’U is conformable, n = 2, p = 2
  • Y’S is not conformable, n = n, p = 2
  • Matrix multiplication is conformable if and only if the number of columns in the first matrix equals the number of rows in the second matrix.
  • Using this property, we find that YW, UU', and U'U are conformable, while YW' and Y'S are not.

Q2. Conformability of b=(Yw)':

Problem Description: Examine the conformability of the transpose of the product b=(Yw)' for matrices Y (n×2) and w (2×1). Provide insights into the resulting dimensions and their significance.

  • b=(Yw)' is conformable since Y is n×2 and w is 2×1. Also, the resulting dimension of b is 2×n.

Q3. First Principal Component:

Problem Description: Given that w is the eigenvector corresponding to the largest eigenvalue, explore how the vector b, derived from the product Yw, contains the first principal component of the data.

  • As w is the eigenvector corresponding to the largest eigenvalue, the vector b contains the first principal component of the data.

Q4. Covariance and Variance Calculations:

Problem Description: Utilize matrix properties to express variables a_i and b_i in terms of U and W. Calculate the variance of a and b, and explore the covariance between them in the context of the sample mean and covariance matrix.

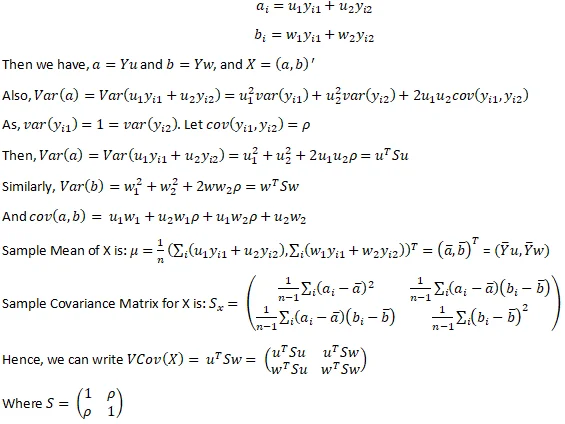
Covariance and Variance Calculations

Q5. Orthogonality:

Problem Description: Investigate the orthogonality of eigenvectors w and u, and explore the implications of u^T w = 0. Discuss the relationships between eigenvectors and eigenvalues.

  • The eigenvectors w and u are orthogonal if u^T w = 0.
  • If u^T w = 0, then u = cv, where v is the eigenvector corresponding to the lower eigenvalue.
  • Additionally, v and w are eigenvectors of S, and Sw = λ_1 w, where λ_1 is the largest eigenvalue.

Note: For brevity, mathematical notations and expressions have been summarized. Detailed derivations and proofs are available in the full solution.