Question 1: Understanding Educational Influences
Problem Description: Investigate the impact of parental factors and cognitive ability on a person's years of schooling. Specifically, explore the significance of the biological father's schooling, the composite measure of cognitive ability, and the biological mother's schooling on the years of schooling.
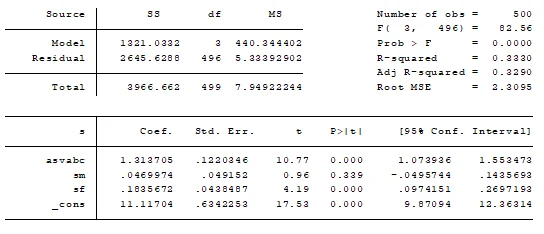
Table 1: Impact of parental factors vs. years of schooling
Answer: The findings reveal a significant positive impact of the biological father's schooling and cognitive ability on education. However, the influence of the biological mother's schooling is considered insignificant.
Question 2: Assessing Model Significance and Power
Problem Description: Evaluate the overall significance of the model in predicting years of schooling. Additionally, analyze the power of the model based on the coefficient of determination (R^2).
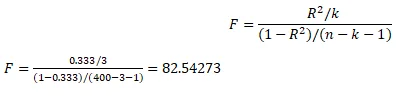
Answer: While the model is statistically significant, the R^2 indicates a relatively low explanatory power, explaining less than half of the total variability in years of schooling.
Question 3: Linking Education and Earnings
Problem Description: Examine the relationship between years of schooling and work experience on earnings. Determine the significance of these factors and the overall model in predicting earnings.
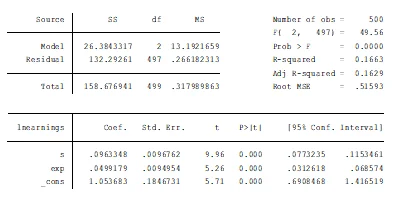
Table 2: Relationship between years of schooling and work experience
Answer: Both schooling and work experience significantly impact earnings, as indicated by t-tests. The overall model is also statistically significant in predicting earnings.
Question 4: Multifaceted Influences on Earnings
Problem Description: Investigate the joint influence of schooling, work experience, gender, and ethnicity on earnings. Determine the significance of each factor and the overall model.
Answer: Schooling, work experience, and gender significantly affect earnings, while ethnicity does not show a significant impact. The overall model is statistically significant.
Question 5: Sensitivity Analysis and Model Changes
Problem Description: Explore how changes in reference categories affect the interpretation of coefficients and statistical tests in the model.
Answer: Most coefficients and statistical tests remain unchanged except for ETHHISP, and the coefficient for ETHWHITE becomes positive.
Question 6: Regression Equation and Gender Interaction
Problem Description: Present a regression equation detailing the relationship between earnings, education, work experience, and gender. Investigate if there is a significant interaction effect between years of schooling and gender.
Answer: The overall model is statistically significant. All variables are statistically significant except ethnicity, indicating a significant interaction between years of schooling and gender.
Question 7: Parameter Comparison
Problem Description: Compare parameters and test hypotheses regarding their equality or difference.
Answer: The null hypothesis is accepted for ASVBAR and rejected for ASVBAR vs. 2 * ASVABPC, indicating different parameter values.
Question 8: Heteroskedasticity Test in S Dimension
Problem Description: Apply the Goldfeld-Quandt test to assess the presence of heteroskedasticity in the S dimension.
Answer: The null hypothesis of homoscedasticity is not rejected, suggesting no evidence of heteroskedasticity in the data.
Question 9: White Test for Heteroskedasticity
Problem Description: Conduct the White test to investigate the presence of heteroskedasticity in the data.
Answer: The null hypothesis of homoscedasticity is not rejected, indicating no evidence of heteroskedasticity in the data.
Question 10: Exogeneity Test
Problem Description: Assess the exogeneity of the variable ASVABC and its correlation with the error term.
Answer: The p-value (0.311) is greater than the significance level, indicating that ASVABC is exogenous and not correlated with the error term. The null hypothesis is not rejected.