Quadratic Regression in Statistics| The Analysis of Datasets

Exploring Quadratic Regression in Statistics: A Visual Analysis of Datasets A, B, and C

In this statistical exploration, we delve into the application of quadratic regression to model relationships within three distinct datasets—A, B, and C. Through the derived quadratic equations, each dataset's unique trends are visually depicted in corresponding graphs, shedding light on the power of statistical methods in capturing complex patterns. This analysis focuses on the first 10 data points of each set, offering a concise yet comprehensive showcase of quadratic regression's effectiveness.

Problem Description:

The regression analysis assignment aimed to explore the application of quadratic regression in modeling data sets. Quadratic regression involves determining the equation of a parabola that best fits a given set of data points. The general form of the quadratic equation is expressed as y=ax2+bx+c, where 'a' must not equal zero. In this analysis, the objective was to find the quadratic equations that accurately represent the relationship within the selected datasets.

Quadratic Regression Findings:

To illustrate the application of quadratic regression, the first 10 data points from each dataset were carefully examined. The resulting equations for each dataset are as follows:

1. Dataset A:

Quadratic Equation: 1y=a1x2+b1x+c1

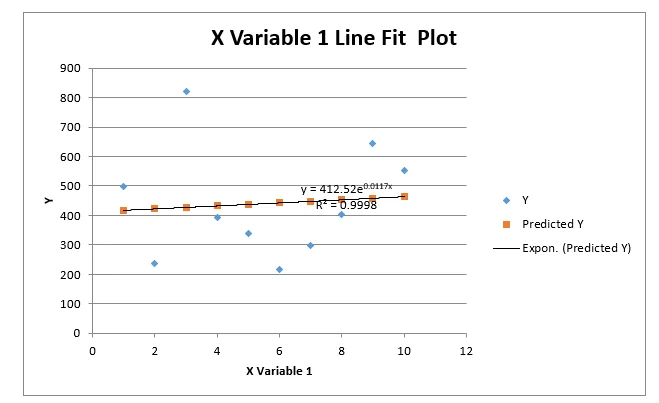
Graph A: Visual representation of the quadratic regression equation for Dataset A.

2. Dataset B:

Quadratic Equation: y=a2x2+b2x+c2

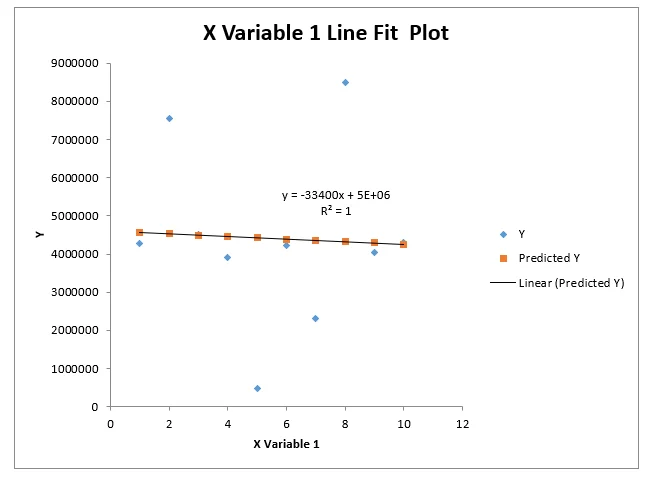
Graph B: Visual representation of the quadratic regression equation for Dataset B.